Movimiento vibratorio amortiguado
Una masa m1 está sujeta al extremo de un resorte flexible
suspendida de un soporte rígido (el techo o cualquier otro). Cuando se cambia
la masa m1 por una masa diferente, pues el alargamiento será obviamente
distinto.
Por la ley de Hooke, el resorte en sí ejerce una fuerza F
opuesta al alargamiento y que es proporcional a su magnitud s.
La ecuación F = ks en donde k es la constante de
proporcionalidad que en diferentes resortes puede o no ser el mismo; el
resorte elástico está caracterizado por el número k.
Por ejemplo si un cuerpo de 10 lb alarga un resorte en ½ ft,
entonces:
10 = k(1/2) implica que k = 20lb/ft
Segunda ley de newton
Después de que m1 se sujeta al resorte, lo alargara en una
magnitud s, éste alcanzará la posición de equilibrio en la cual el peso W es
equilibrado por la fuerza de restitución ks.
Ecuación del peso W =
mg
Donde g es la gravedad 32 ft / s^2
La masa m puede medirse en kg, g, o slugs
El equilibrio es mg =
ks o mg – ks = 0
Ahora si la masa m se desplaza de su posición de equilibrio
en una magnitud x y después se suelta, la fuerza correspondiente al movimiento
está dada por la segunda ley de newton, F
= ma
Donde a es la aceleración
Y en el caso del movimiento vibratorio
amortiguado, actúan fuerzas de amortiguación que actúan sobre el cuerpo y son
proporcionales a una potencia de la velocidad instantánea.
Esto se debe a que el sistema puede estar sumergido en un medio viscoso o conectado a un mecanismo de amortiguación.
Ésta fuerza está dado por un múltiplo constante de 
Cuando no actúen otras fuerzas sobre el
sistema se obtiene que
Cuando no actúen otras fuerzas sobre el
sistema se obtiene que
En donde
es una constante de amortiguación positiva y
el signo negativo se debe a que la fuerza amortiguadora está opuesta al
movimiento. De igual manera el signo negativo en la fuerza de restitución k
actuará opuesta al movimiento.
Ahora consideraremos la siguiente
convención para querer resolver un problema de éste tipo:
Cuando el desplazamiento a partir de la
posición de reposo es hacia arriba se considera un signo negativo.
Cuando el desplazamiento a partir de la
posición de reposo es hacía abajo se considera un signo positivo.
Ahora bien, para poder explicarles cómo se soluciona una ecuación
diferencial de segundo orden supongamos que nos dan los valores iniciales.
Una masa de ¼ de slug
= 2
k = 4
Construimos la ecuación diferencial.
¡LISTO TENEMOS LA ECUACIÓN DIFERENCIAL!
Pero esa ecuación diferencial se ve muy
fea, necesitamos simplificarla y obtener su solución.
Simplificada quedaría de éste modo:
Ahora bien, el método que usaré a
continuación lo aprendí en mi curso de ecuaciones diferenciales de mi carrera
en la universidad.
Donde vea
(que es la derivada) pongo una D y
si veo
(que es la segunda derivada) pongo D^2.
Nótese que en las derivadas no está la x , esto es por conveniencia para que la
ecuación quede de éste modo:
Nos damos cuenta que la ecuación que
tenemos es un simple ecuación cuadrática de la forma:
Donde se puede resolver por varios métodos.
Ahora solamente se resuelve la parte
entre paréntesis:
Donde D = -4, -4
En éste ejemplo tenemos raíces múltiples,
es decir, una raíz es -4 y la otra de igual manera es -4 por el simple hecho de ser un binomio al cuadrado. En ese caso la solución
que daría de éste modo
Esa sería la solución a nuestra ecuación
diferencial dada al inicio, en nuestro caso el tipo de movimiento amortiguado:
es críticamente amortiguado. Se preguntarán ¿A qué se refiere con los tipos de
movimiento amortiguado?
Dada una ecuación diferencial:
Donde a
y b son constantes.
Y las raíces correspondientes a D serían:
En donde
a/2 se usa por conveniencia algebraica
en la que no afecta al resultado; y según el signo algebraico
Podemos distinguir 3 casos posibles
Caso
I:
El movimiento está sobre-amortiguado puesto que el coeficiente de amortiguación es grande en comparación de la
constante k del resorte. La solución quedaría de éste modo:
Ésta ecuación representa un movimiento
suave y no oscilatorio.
Nótese
que cuando se obtiene la ecuación de la forma
Es un binomio cuadrado no perfecto.
Caso II:
El sistema está críticamente amortiguado
ya que una pequeña disminución de la fuerza de amortiguación causaría un
movimiento oscilatorio o bien el coeficiente de amortiguación es igual a la
constante del resorte. La solución sería.
Es un binomio al cuadrado.
Caso III:
El sistema está subamortiguado, ya que la
constante de amortiguación es pequeña a comparación del resorte
Las raíces D1 y D2 son complejas.
Y la solución general será de éste modo:
éste movimiento describe una oscilación que disminuye conforme pasa el tiempo.
Bueno, aquí está la explicación de los diferentes 3 casos que puede haber en el movimiento vibratorio amortiguado. A mi parecer el caso III es el más interesante, ya que puede ser aplicado por ejemplo en los saltos en bongie. Ahora veo porque no muere la gente al saltar, gracias a las ecuaciones diferenciales.
En un post a futuro explicaré la solución de problemas enunciados, ya que desde el principio el problema muchas veces te da las variables en si.
Gracias por su tiempo y nos vemos en el siguiente post.
Ah! por cierto mañana es la marcha antipeñanieto aquí en Qro. iré y posteriormente les dejaré la crónico.
Buenas noches.
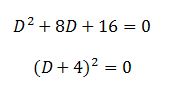
No hay comentarios:
Publicar un comentario